Cálculo diferencial en un semiespacio cerrado
Sean ![]() un espacio afín normado de dimensión finita,
un espacio afín normado de dimensión finita, ![]() su espacio vectorial asociado,
su espacio vectorial asociado, ![]() un hiperplano de
un hiperplano de ![]() ,
,
![]() y
y ![]() un semiespacio de
un semiespacio de ![]() de borde
de borde ![]() .
.
Un referencial
![]() de
de ![]() lo llamaremos REFERENCIAL ADAPTADO AL SEMIESPACIO
lo llamaremos REFERENCIAL ADAPTADO AL SEMIESPACIO ![]() si
si
![]() ,
,
![]() es una base de
es una base de ![]() y el vector
y el vector ![]() apunta hacia el semiespacio
apunta hacia el semiespacio ![]() .
.
Sean
![]() las correspondientes funciones coordenadas:
las correspondientes funciones coordenadas:
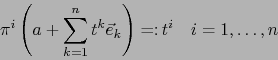
Sea
![]() un conjunto abierto con respecto a
un conjunto abierto con respecto a
![]() . Si
. Si
![]() , entonces
, entonces ![]() también es un abierto en
también es un abierto en ![]() . Lo llamaremos ABIERTO DE PRIMERA ESPECIE en
. Lo llamaremos ABIERTO DE PRIMERA ESPECIE en
![]() . En el caso
contrario
. En el caso
contrario
![]() (por cierto
(por cierto
![]() es un conjunto abierto con respecto
a
es un conjunto abierto con respecto
a ![]() ) y los puntos de
) y los puntos de ![]() no son puntos interiores de
no son puntos interiores de ![]() con respecto a
con respecto a ![]() . En este caso diremos que
. En este caso diremos que ![]() es un ABIERTO DE SEGUNDA ESPECIE en
es un ABIERTO DE SEGUNDA ESPECIE en
![]() .
.