




Siguiente: Aplicaciones de clase
Arriba: Cálculo diferencial en un
Anterior: Diferencial de una aplicación
Definición 6.4
Si
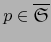 y
y 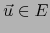 definimos
definimos
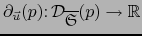 por:
por:
Del teorema 4.6.4 se desprende sin más:
Teorema 6.7
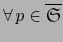 y
y
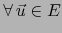 vale:
vale:
Lema 6.1
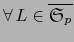 se tiene
se tiene
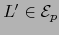 .
.
Demostración
Debemos probar que la funcional
 goza de las tres propiedades
leibnizianas.
goza de las tres propiedades
leibnizianas.
- Sean
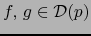 y
y
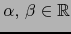 .
. 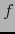 es una función
es una función
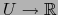 y
y 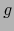 es una función
es una función
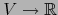 , donde
, donde 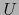 y
y  son vecindades abiertas del punto
son vecindades abiertas del punto  en
en  .
. 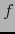 y
y 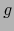 son diferenciables
en
son diferenciables
en  . Con las notaciones de la definición 4.6.5 se verifica:
. Con las notaciones de la definición 4.6.5 se verifica:
pues ambos miembros de esta relación son funciones cuyo dominio es
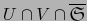 . Usando
la definición 4.6.5 y la propiedad leibniziana 1) de
. Usando
la definición 4.6.5 y la propiedad leibniziana 1) de  obtenemos:
obtenemos:
comprobando la propiedad leibniziana 1) para  .
.
- Sean
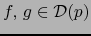 . Vale:
. Vale:
pues, con las notaciones del inciso a) ambos miembros de esta relación son funciones de dominio
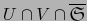 . Usando
la definición 4.6.5 y la propiedad leibniziana 2) de
. Usando
la definición 4.6.5 y la propiedad leibniziana 2) de  conseguimos:
conseguimos:
comprobando la propiedad leibniziana 2) para 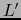 .
.
- Sean
 tal que
tal que 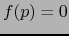 y
y
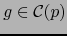 luego:
luego:
 ,
,
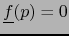 y
y
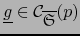 . Como en el inciso
b):
. Como en el inciso
b):
Por la definición 4.6.5 y la propiedad leibniziana 3) de  tenemos:
tenemos:
Viene, pues, comprobada la propiedad leibniziana 3) de 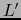 .
.

Demostración
La aplicación
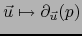 es una aplicación lineal
del espacio vectorial
es una aplicación lineal
del espacio vectorial  sobre el espacio vectorial
sobre el espacio vectorial
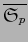 . Esto se prueba exactamente
como en el inciso a) del teorema 4.3.10.
. Esto se prueba exactamente
como en el inciso a) del teorema 4.3.10.
Inyectividad de la aplicación
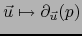 .
Sea
.
Sea 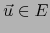 tal que se cumpla
tal que se cumpla
 . Consideremos un referencial
. Consideremos un referencial
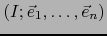 en
en  y sean las funciones
y sean las funciones
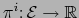 ,
, 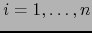 , las coordenadas correspondientes
como en el enunciado. Pongamos
, las coordenadas correspondientes
como en el enunciado. Pongamos
![$\forall \, i \in [\![ 1 , n ]\!]$](img2676.png) sea
sea
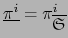 .
. 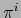 es una ampliación diferenciable
de
es una ampliación diferenciable
de
 . En particular
. En particular
 . Luego
. Luego
![$\forall \, i \in [\![ 1 , n ]\!]$](img2676.png)
Así pues,  . Por lo tanto, la aplicación:
. Por lo tanto, la aplicación:
es una aplicación lineal inyectiva de  en
en
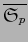 .
.
Superyectividad de la aplicación
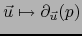 .
Sea
.
Sea
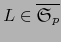 un vector tangente arbitrario a
un vector tangente arbitrario a
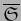 en el punto
en el punto  . Con
las notaciones del lema 4.6.1 sea
. Con
las notaciones del lema 4.6.1 sea 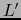 el correspondiente elemento de
el correspondiente elemento de 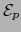 . Sea
. Sea
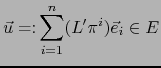 .
.
Por el teorema 4.3.10 vale
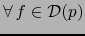
Sea  un elemento arbitrario de
un elemento arbitrario de
 . Por la definición
4.6.1, existe un
. Por la definición
4.6.1, existe un
 tal que el dominio de
tal que el dominio de 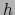 es la intersección de aquel de
es la intersección de aquel de
 con
con
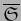 y
y 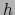 es retricción de
es retricción de  .
Por la definición de
.
Por la definición de 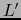 :
:
luego
 .
.
Así pues, la aplicación
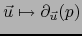 es una aplicación lineal superyectiva
de
es una aplicación lineal superyectiva
de  sobre el espacio vectorial
sobre el espacio vectorial
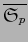 .
.






Siguiente: Aplicaciones de clase
Arriba: Cálculo diferencial en un
Anterior: Diferencial de una aplicación
Guillermo M. Luna
2009-06-14
![]() goza de las tres propiedades
leibnizianas.
goza de las tres propiedades
leibnizianas.
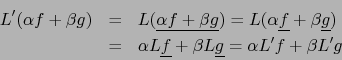
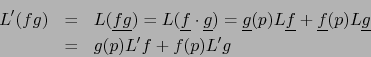
![]() un referencial en
un referencial en ![]() y sean
y sean
![]() las coordenadas
con respecto a dicho referencial, es decir:
las coordenadas
con respecto a dicho referencial, es decir:
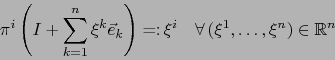
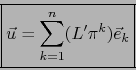
![]() es una aplicación lineal
del espacio vectorial
es una aplicación lineal
del espacio vectorial ![]() sobre el espacio vectorial
sobre el espacio vectorial
![]() . Esto se prueba exactamente
como en el inciso a) del teorema 4.3.10.
. Esto se prueba exactamente
como en el inciso a) del teorema 4.3.10.
![]() .
Sea
.
Sea ![]() tal que se cumpla
tal que se cumpla
![]() . Consideremos un referencial
. Consideremos un referencial
![]() en
en ![]() y sean las funciones
y sean las funciones
![]() ,
, ![]() , las coordenadas correspondientes
como en el enunciado. Pongamos
, las coordenadas correspondientes
como en el enunciado. Pongamos

![]() .
Sea
.
Sea
![]() un vector tangente arbitrario a
un vector tangente arbitrario a
![]() en el punto
en el punto ![]() . Con
las notaciones del lema 4.6.1 sea
. Con
las notaciones del lema 4.6.1 sea ![]() el correspondiente elemento de
el correspondiente elemento de ![]() . Sea
. Sea
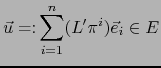 .
.
![]()
![]() es una aplicación lineal superyectiva
de
es una aplicación lineal superyectiva
de ![]() sobre el espacio vectorial
sobre el espacio vectorial
![]() .
.
![]()