Siguiente: La funcional Arriba: Cálculo diferencial en un Anterior: Cálculo diferencial en un

Diferencial de una aplicación en un punto de $\cal H$

Sean $V$ un abierto con respecto a $\overline{ \mbox{\frakiii S}}$, $\cal F$ otro espacio afín normado de espacio vectorial asociado $F$ y $\varphi$ una aplicación $V \to \cal F$. Sea $p\in V$. Si $V$ es un abierto de primera especie o de segunda pero $p \notin V \cap \cal H$ la diferencial $d\varphi(p) \in {\cal L}(E,F)$ ya está definida (a suponer que existe). Queda el caso de ser $V$ de segunda especie y $p \in V \cap \cal H$.

Nota
A continuación la abreviación ``C.D.'' significará: ``en el sentido del Cálculo Diferencial''.

Definición 6.1   Sea $V$ un abierto de segunda especie en $\overline{ \mbox{\frakiii S}}$ y sea $\varphi$ una aplicación $V \to \cal F$. Sea $p \in V \cap \cal H$. Se dice que la APLICACIÓN ES DIFERENCIABLE EN EL PUNTO $p$ si existen un abierto $\tilde V$ de $\cal E$ que cumpla la condición ${\tilde V} \cap \overline{ \mbox{\frakiii S}} = V$ y una ampliación $\tilde \varphi$ de $\varphi$ a $\tilde V$ tal que $\tilde \varphi$ es diferenciable (C.D.) en el punto $p$.

Observación 1

Para todo abierto $V$ de segunda especie en $\overline{ \mbox{\frakiii S}}$ existe un abierto $\widetilde V$ de $\cal E$ tal que $V=\widetilde V \cap \overline{\mbox{\frakiii S}}$.

Supongamos que $\varphi$ es diferenciable en el punto $p \in V \cap \cal H$ según la definición 4.6.1. Debido al carácter local de la diferenciabilidad podemos suponer siempre que la amplicación $\widetilde \varphi$ de $\varphi$ exigida por la definición está definida en cualquier tal abierto $\widetilde V$ elegido arbitrariamente.

Observación 2

Con las notaciones de la definición 4.6.1, supongamos $\varphi$ diferenciable en el punto $p$. $\forall \, \vec u \in E$ vale:

$$d {\tilde \varphi}(p) \vec u = \partial_{\vec u} {\tilde \var... ...} {{\tilde \varphi}(p+ t \vec u) - {\tilde \varphi}(p) \over t}$$

Restringiendo el recorrido de $t$ obtenemos:

$$d {\tilde \varphi} (p) \vec u = \left\{ \begin{array}{ll} {... ...cm}\ -\vec u\mbox{ apunta hacia \frakiii S} \end{array}\right.$$ (1)

La fórmula (1) muestra que, de existir la aplicación lineal $d \tilde \varphi (p) \colon E \to F$, depende solamente de $\varphi$ y no de la ampliación elegida $\tilde \varphi$. La llamaremos la DIFERENCIAL DE LA APLICACIÓN EN EL PUNTO y la designaremos simplemente por $d \varphi(p)$.

Los dos teoremas a continuación son evidentes:

Teorema 6.1   Si con las notaciones de arriba, $\varphi \colon V \to \cal F$ es diferenciable en un punto $p \in V \cap \cal H$, $\varphi$ es continua en el punto p.

Teorema 6.2 (Carácter local de la diferenciación)   Sea $p \in \cal H$. Sean V, W abiertos de segunda especie en $\overline{ \mbox{\frakiii S}}$ tales que $p \in W \subset V$. Sea $\varphi \colon V \to \cal F$. $\varphi$ es diferenciable en el punto $p$ si y sólo si la restricción $\varphi_W$ de $\varphi$ a $W$ es diferenciable en el punto p y entonces:

$$d \varphi(p) = d \varphi_W (p).$$

Teorema 6.3   Sean $S,\, T$ abiertos en sendos semiespacios cerrados $\overline{\mbox{\frakiii S}}^{(n)}$, $\overline{\mbox{\frakiii S}}^{(m)}$ en espacios afines normados ${\cal E}_n$, ${\cal E}_m$ de dimensiones respectivos $n,\,m$. Sean $\cal F$ un espacio afín normado, $\varphi$ una aplicación $S \to T$ y $\psi$ una aplicación $T \to \cal F$. Se supone $\varphi$ diferenciable en un punto $p \in S$ y $\psi$ diferenciable en el punto $\varphi (p) \in T$. La aplicación $\psi \circ \varphi \colon S \to \cal F$ es diferenciable en el punto p y vale:

$$\fbox{${\displaystyle d (\psi \circ \varphi)(p) = d\psi \left( \varphi(p) \right) \circ d \varphi (p) }$}$$

(REGLA DE LA CADENA PARA SEMIESPACIOS CERRADOS).

Demostración
La hipótesis significa que existen abiertos $\widetilde{S},\widetilde{T}$ en sendos espacios ${\cal E}_n$, ${\cal E}_m$ tales que $\widetilde{S} \cap \overline{\mbox{\frakiii S}}^{(n)} = S$, $\widetilde{T} \cap \overline{\mbox{\frakiii S}}^{(m)} = T$ y ampliaciones $\widetilde{\varphi}, \widetilde{\psi}$ de las aplicaciones $\varphi,\psi$ a los abiertos $\widetilde{S}$, $\widetilde T$ tales que $\widetilde \varphi$ es diferenciable (C.D.) en el punto $p$ y $\widetilde \psi$ es diferenciable (C.D.) en el punto $\varphi(p)$. A mayor abundamiento $\widetilde \varphi$ es continua en $p$. Existe, pues, una vecindad abierta $\widetilde V$ de $p$ en ${\cal E}_n$ contenida en $\widetilde S$ tal que $\widetilde{\varphi}( \widetilde{V})$ está contenido en la vecindad $\widetilde T$ de $\varphi(p)$. Por el carácter local de la diferencial la restricción de $\widetilde \varphi$ a $\widetilde V$, que seguimos designando por $\widetilde \varphi$, es diferenciable (sin cambio de diferencial) en el punto $p$. En virtud del teorema 4.4.4 (``Regla de la cadena'') la aplicación $\widetilde{\psi} \circ \widetilde{\varphi} \colon \widetilde{V} \to \cal F$ es diferenciable en $p$ y vale:

$$d (\widetilde{\psi} \circ \widetilde{\varphi} ) (p) = d \wid... ...\widetilde{\varphi} (p) \right) \circ d \widetilde{\varphi}(p)$$ (2)

Al restringir $\varphi$ al abierto $V = \colon \widetilde{V} \cap \overline{\mbox{\frakiii S}}^{(n)}$ de $\overline{\mbox{\frakiii S}}^{(n)}$ contenido en $S$, la relación (2) significa que $\psi\circ \varphi$ es diferenciable en el punto $p$ y vale:

$$d \left( \psi \circ \varphi \right) (p) = d \psi \left( \varphi (p) \right) \circ d \varphi(p)$$

$\quad\Box$

Se generaliza también el teorema 4.3.5, a saber:

Teorema 6.4   Sean $V$ un abierto de segunda especie en $\overline{ \mbox{\frakiii S}}$ y $p \in V \cap \cal H$. Sean f,g funciones $V \to {\mathbb{R}}$

1. Si $f$ y $g$ son diferenciables en el punto $p$, $\forall \, \alpha,\, \beta \in {\mathbb{R}}$ la función $\alpha f + \beta g$ será diferenciable en el punto $p$ y valdrá :
   
   $$\fbox{${\displaystyle d(\alpha f + \beta g) (p) = \alpha d f(p) + \beta d g(p)}$}$$
   
   

2. Si $f$ y $g$ son diferenciables en $p$, también la función $fg$ es diferenciable en $p$ y vale:
   
   $$\fbox{${\displaystyle d(f g) (p) = g(p) d f(p) + f(p) d g(p)}$}$$
   
   

3. Si $f$ es diferenciable en $p$ y satisface $f(p) =0$, siendo además $g$ continua en el punto $p$, la función $fg$ es diferenciable en el punto $p$ y vale:
   
   $$\fbox{${\displaystyle d(fg) (p) = g(p)d f(p)}$}$$
   
   

Demostración
En los casos a) y b) cabe suponer que existe un abierto $W$ de $\cal E$ tal que $W \cap \overline{\mbox{\frakiii S}} =V$ y ampliaciones $\tilde f,\, \tilde g$ de sendas funciones $f$ y $g$ al abierto $W$, ambas diferenciables en el punto $p$. En los incisos a) y b) a continuación se supone que éste es el caso:

1. Por el teorema 4.3.5, $\forall \, \alpha,\, \beta \in {\mathbb{R}}$ es diferenciable en $p$ la función $\alpha \tilde f + \beta \tilde g$ y vale:
   

   $$d (\alpha \tilde f + \beta \tilde g)(p) = \alpha d \tilde f (p) + \beta d \tilde g (p)$$ (3)

   
   
   Ya que $\alpha \tilde f + \beta \tilde g$ es una ampliación de $\alpha f + \beta g$ al abierto $W$, se sigue de ahí que $\alpha f + \beta g$ es diferenciable en $p$ (según la definición 4.6.2) y el primer miembro de (3) es $d(\alpha f + \beta g)(p)$. El segundo miembro es $\alpha d f(p) + \beta dg(p)$ luego por (3):
   
   $$d( \alpha f + \beta g)(p) = \alpha df(p) + \beta dg(p)$$
   
   
   como afirmamos.
2. Por el teorema 4.3.5, $\tilde f \tilde g$ es diferenciable en $p$ y vale:
   

   $$d (\tilde f \tilde g) (p) = \tilde g(p) d \tilde f(p) + \tilde f(p) d \tilde g(p)$$ (4)

   
   
   Pero $\tilde f \tilde g$ es una ampliación de la función $fg$ al abierto $W$. Así pues, por (4) la función $fg$ es diferenciable en $p$ (según la definición 4.6.2) y el primer miembro de (4) es $d(fg)(p)$. El segundo miembro es $g(p) df(p) + f(p)dg(p)$. Por (4) vale pues:
   
   $$d(fg)(p) = g(p) df(p) + f(p) dg(p)$$
   
   
   como anunciamos.
3. Supongamos ahora que $f$ es diferenciable en $p$, $f(p) =0$ y $g$ es continua en el punto $p$. Vamos a construir un abierto $W$ de $\cal E$ tal que $W \cap \overline{\mbox{\frakiii S}} =V$ y una ampliación $\tilde g$ de $g$ continua en el punto $p$. Fijemos un vector $\vec u \in E$ que apunta hacia el subespacio . Sea $\sigma \colon {\cal E} \to {\cal E}$ la aplicación:
   
   $$\sigma (h + t \vec u ) = \colon h - t \vec u \quad \forall \, h \in {\cal H} \; \forall \, t \in {\mathbb{R}}$$
   
   
   $\sigma$ es un homeomorfismo afín de $\cal E$ sobre $\cal E$. Preserva todo punto de $\cal H$ y transforma en el semiespacio opuesto $\mbox{\frakiii S}^\prime$. Definamos:
   

   $$W = \colon V \cup \sigma (V)$$ (5)

   
   
   Puesto que $V$ es un abierto en $\overline{ \mbox{\frakiii S}}$ y $\sigma$ induce un homeomorfismo de $\overline{ \mbox{\frakiii S}}$ sobre $\overline{\mbox{\frakiii S}^\prime}$, $\sigma (V)$ es abierto en $\overline{\mbox{\frakiii S}^\prime}$. El par $( \overline{\mbox{\frakiii S}}, \overline{\mbox{\frakiii S}^\prime})$ es un recubrimiento cerrado finito de $\cal E$, luego (5) entraña que $W$ es abierto en $\cal E$. Claramente: $W \cap \overline{\mbox{\frakiii S}} =V$. Sea $\tilde g \colon W \to {\mathbb{R}}$ la función definida por:
   
   $$\tilde g (q) = \colon \left\{ \begin{array}{rl} g(p) & \mbox... ...c \sigma)(q) & \mbox{si } q \in \sigma (V) \end{array}\right.$$
   
   
   La definición de $\tilde g$ es unívoca. $\tilde g$ es una ampliación de $g$ al abierto $W$ de $\cal E$. Las restricciones de $\tilde g$ a $V$ y $\sigma (V)$, que constituyen un recubrimiento cerrado finito de $W$, son continuas en $p$. Luego $\tilde g$ es continua en el punto $p$.

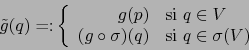
   En virtud de la observación 1 después de la definición 4.6.1 existe $\widetilde{f} \colon W \to {\mathbb{R}}$, una ampliación de $f$ a $W$, diferenciable en el punto $p$.

   Por el teorema 4.3.5, la función $\widetilde{f} \widetilde{g}$ es diferenciable en el punto $p$ y vale:
   

   $$d (\widetilde{f} \widetilde{g} ) (p) = \widetilde{g} (p) d \widetilde{f} (p)$$ (6)

   
   
   Pero $\widetilde{f} \widetilde{g}$ es una ampliación de $fg$ al abierto $W$ de $\cal E$. Así pues, según la definición 4.6.1 la función $fg$ es diferenciable en $p$ y el primer miembro de (6) no es otro que la diferencial $d(fg)(p)$. El segundo miembro de (6) vale $g(p) df(p)$. Así pues, por (6):
   
   $$d\left( fg \right) (p) = dg(p) df(p)$$
   
   

$\quad\Box$

Imitando las definiciones 4.3.2 adoptamos la siguiente:

Definición 6.2   Sea $p \in \overline{\mbox{\frakiii S}}$. Se llama FUNCIÓN LOCAL EN SOBRE $\overline{ \mbox{\frakiii S}}$ a una función $f \colon V \to {\mathbb{R}}$ donde $V$ es un abierto con respecto a $\overline{ \mbox{\frakiii S}}$ que contiene el punto $p$ (y depende de $f$).

Designaremos por ${\cal F}_{\overline{\mbox{\fraki S}}} (p)$ el conjunto de todas las funciones locales en $p$ sobre $\overline{ \mbox{\frakiii S}}$, por ${\cal C}_{\overline{\mbox{\fraki S}}} (p)$ el conjunto de todas las funciones locales en $p$ sobre $\overline{ \mbox{\frakiii S}}$ continuas en el punto $p$ y por ${\cal D}_{\overline{\mbox{\fraki S}}} (p)$ el conjunto de las funciones locales en $p$ sobre $\overline{ \mbox{\frakiii S}}$ diferenciables en el punto p.

Claramente:

$$\fbox{${\displaystyle {\cal D}_{\overline{\mbox{\fraki S}}} (... ...ki S}}} (p) \subset{\cal F}_{\overline{\mbox{\fraki S}}} (p)}$}$$

Exactamente como en las definiciones 4.3.2, si $f,\, g \in {\cal F}_{\overline{\mbox{\fraki S}}} (p)$ y $\alpha, \, \beta \in {\mathbb{R}}$ definimos las funciones $\alpha f + \beta g$ y $fg$ en ${\cal F}_{\overline{\mbox{\fraki S}}} (p)$. Los conjuntos ${\cal C}_{\overline{\mbox{\fraki S}}} (p)$ y ${\cal D}_{\overline{\mbox{\fraki S}}} (p)$ son cerrados respecto a estas operaciones. También, debido al teorema 4.6.4 vale:

Teorema 6.5   Si $f \in {\cal D}_{\overline{\mbox{\fraki S}}} (p)$ es tal que $f(p) =0$ y $g \in {\cal C}_{\overline{\mbox{\fraki S}}} (p)$, entonces $fg \in {\cal D}_{\overline{\mbox{\fraki S}}} (p)$.

Imitando la definición 4.3.4 sentamos:

Definición 6.3   Si $p \in \overline{\mbox{\frakiii S}}$ se llama VECTOR TANGENTE AL SEMIESPACIO CERRADO $\overline{ \mbox{\frakiii S}}$ en el punto $p$ a toda funcional $L \colon {\cal D}_{\overline{\mbox{\fraki S}}} (p) \to {\mathbb{R}}$ que goza de las tres propiedades leibnizianas:

$$\fbox{${\displaystyle \begin{array}{ll} \mbox{\em 1)} & L (\a... ...S}}} (p)\mbox{\em \ entonces } L(fg) = g(p) L f \end{array} }$}$$

Designaremos por $\overline{\mbox{\frakiii S}_p}$ al conjunto de todos los vectores tangentes al semiespacio cerrado $\overline{ \mbox{\frakiii S}}$ en el punto p.

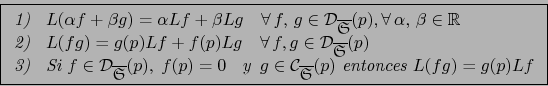
La observación después de la definición 4.3.4 sigue válida en el presente contexto. Es decir:

Si $L \in \overline{\mbox{\frakiii S}_p}$ y $f \in {\cal D}_{\overline{\mbox{\fraki S}}} (p)$ es constante en su dominio vale: $L f = 0$.

Teorema 6.6 (definición)   $\overline{\mbox{\frakiii S}_p}$ es un espacio vectorial real. Se llama ESPACIO VECTORIAL TANGENTE AL SEMIESPACIO CERRADO #MATH4998# EN EL PUNTO .

La demostración es idéntica a la del teorema 4.3.9.

Siguiente: La funcional Arriba: Cálculo diferencial en un Anterior: Cálculo diferencial en un