La palabra FUNCIONAL se usa comúnmente para designar a una aplicación generalmente de valores en ![]() o
o ![]() y cuyo
dominio es algún conjunto de ``funciones''.
y cuyo
dominio es algún conjunto de ``funciones''.
A las propiedades a), b) y c) nos referiremos como las tres PROPIEDADES LEIBNIZIANAS de la funcional
Demostración
Teniendo en cuenta el carácter local de la diferenciación, vemos que el teorema 4.3.8 es el mismo,
a menos de la notación, que el teorema 4.3.6.
![]()
Nota
Puede sorprender en la definición 4.3.2 la restricción, a priori injustificada,
a espacios afines de dimensión finita. Pero esta restricción es parte de la hipótesis en el
importante teorema 4.3.10 (Teorema de Ellis), por lo cual resulta prudente la limitación que nos impusimos.
Observación
Sea ![]() un vector tangente a
un vector tangente a ![]() en
en ![]() . Designemos por
. Designemos por ![]() la función constante de valor 1
la función constante de valor 1
![]() , donde
, donde
![]() es una vecindad abierta de
es una vecindad abierta de ![]() en
en ![]() .
.
Vale ![]() , de donde por la propiedad leibniziana b) de
, de donde por la propiedad leibniziana b) de ![]() :
:
Demostración
Sean ![]() vectores tangentes a
vectores tangentes a ![]() en
en ![]() y sean
y sean
![]() . Debemos probar que la funcional
. Debemos probar que la funcional
![]() (definida por
(definida por
![]()
![]() ,
,
![]() ) es también un vector
tangente a
) es también un vector
tangente a ![]() en
en ![]() , vale decir posee las tres propiedades leibnizianas. Ahora bien:
, vale decir posee las tres propiedades leibnizianas. Ahora bien:
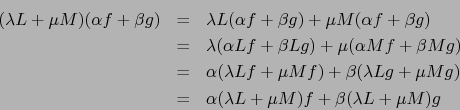
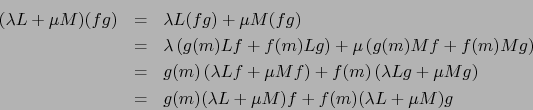
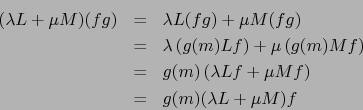
Sea
![]() un referencial en
un referencial en ![]() y sean
y sean
![]()
![]() las ``coordenadas'' con respecto a dicho referencial, es decir:
las ``coordenadas'' con respecto a dicho referencial, es decir:


Demostración
Sean
![]() y
y
![]() .
.
![]() vale en
virtud de la linealidad de la aplicación
vale en
virtud de la linealidad de la aplicación
![]() (observación 2 después
del teorema 4.3.1):
(observación 2 después
del teorema 4.3.1):

Introduzcamos un referencial
![]() y las correspondientes coordenadas
y las correspondientes coordenadas
![]() . Sea
. Sea
![]() .
.
![]() tenemos
tenemos
![]() , de donde, si
, de donde, si
![]() :
:
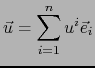 un vector de
un vector de
Sea
![]() arbitrario.
arbitrario. ![]() es una función
es una función
![]() , donde
, donde
![]() es una vecindad abierta del punto
es una vecindad abierta del punto ![]() en
en ![]() .
.
Por definición de la diferencial (fórmula (6) de la observación 1, después del teorema 4.3.1) podemos escribir
![]() :
:
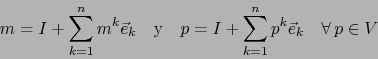

Sea ![]() un vector tangente arbitrario a
un vector tangente arbitrario a ![]() en
en ![]() , elemento de
, elemento de ![]() .
Aplicando
.
Aplicando ![]() a los dos miembros de (27) obtenemos por la propiedad leibniziana a) de
a los dos miembros de (27) obtenemos por la propiedad leibniziana a) de ![]() y la observación después
de la definición 4.3.4:
y la observación después
de la definición 4.3.4:

El teorema de Ellis dice esencialmente que todos los espacios vectoriales tangentes ![]() son canónicamente
isomorfos al espacio vectorial
son canónicamente
isomorfos al espacio vectorial ![]() , asociado al espacio afín
, asociado al espacio afín ![]() . Pueden todos identificarse con el espacio vectorial
. Pueden todos identificarse con el espacio vectorial
![]() .
.
Como consecuencia inmediata del teorema 4.3.10 notamos también que: