Para la demostración de los resultados de topología general citados en este ejemplo referimos a [7] y [25]. Empezamos por recordar dos resultados sobre espacios topológicos cuocientes.
Resultado 1. Sean ![]() un espacio topológico,
un espacio topológico, ![]() una relación de equivalencia en
una relación de equivalencia en ![]() y
y
![]() el espacio topológico cuociente del espacio
el espacio topológico cuociente del espacio ![]() por la relación de equivalencia
por la relación de equivalencia
![]() . Sea
. Sea
![]() la proyección canónica. Sea
la proyección canónica. Sea ![]() una
aplicación de
una
aplicación de ![]() en un espacio topológico
en un espacio topológico ![]() .
.
![]() es continua si y sólo si la aplicación
es continua si y sólo si la aplicación
![]() es continua.
es continua.
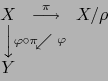
Resultado 2. Con las notaciones del resultado 1. Sean ![]() una parte de
una parte de ![]() ,
, ![]() la relación
de equivalencia inducida por
la relación
de equivalencia inducida por ![]() sobre
sobre ![]() y
y ![]() la proyección canónica
del espacio topológico
la proyección canónica
del espacio topológico ![]() sobre el espacio cuociente
sobre el espacio cuociente ![]() . Sea
. Sea ![]() la restricción
de
la restricción
de ![]() al conjunto
al conjunto ![]() . Existe una única aplicación
. Existe una única aplicación
![]() que hace
conmutativo el diagrama:
que hace
conmutativo el diagrama:
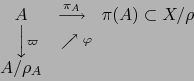
Nota
La condición sobre ![]() en ese enunciado es meramente suficiente. Existe una condición
necesaria y suficiente, pero aquí no la necesitamos.
en ese enunciado es meramente suficiente. Existe una condición
necesaria y suficiente, pero aquí no la necesitamos.
Si
![]() , designamos por
, designamos por
![]() el conjunto de todos los
subespacios vectoriales de dimensión
el conjunto de todos los
subespacios vectoriales de dimensión ![]() en
en
![]() .
.
El objeto de este ejemplo es dotar
![]() de una estructura de variedad
de una estructura de variedad ![]() .
Para determinar un elemento
.
Para determinar un elemento
![]() damos una base
damos una base
![]() de
de
![]() . Ponemos:
. Ponemos:
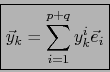
La matriz
![]() es una matriz de
tipo
es una matriz de
tipo
![]() de rango
de rango ![]() .
.
Consideremos ahora otra base
![]() de
de ![]() y sea
y sea
![]() la correspondiente
matriz
la correspondiente
matriz
![]() .
Se verifican las relaciones de la forma:
.
Se verifican las relaciones de la forma:
Al tomar las componentes de los dos miembros de (10) con respecto a la base natural
![]() de
de
![]() , obtenemos las relaciones equivalentes:
, obtenemos las relaciones equivalentes:
Si
![]() y
y ![]() es una matriz de tipo
es una matriz de tipo ![]() inversible, también
inversible, también
![]() .
.
Si
![]() escribamos
escribamos
![]() si existe
si existe ![]() , matriz
, matriz ![]() inversible, tal que
inversible, tal que
![]() .
.
Vimos arriba que toda matriz
![]() determina un subespacio
de dimensión
determina un subespacio
de dimensión ![]() de
de
![]() , elemento de
, elemento de
![]() , a saber, la familia
de las
, a saber, la familia
de las ![]() columnas de
columnas de ![]() constituye una base de dicho subespacio. De las relaciones
equivalentes (10) y (11) se desprende que dos matrices
constituye una base de dicho subespacio. De las relaciones
equivalentes (10) y (11) se desprende que dos matrices
![]() determinan el mismo elemento de
determinan el mismo elemento de
![]() si y sólo si
si y sólo si
![]() o sea
o sea
![]() . Dicho elemento de
. Dicho elemento de
![]() depende pues
solamente de la clase de equivalencia
depende pues
solamente de la clase de equivalencia
![]() .
.
La aplicación que a
![]() le asigna el subespacio de
le asigna el subespacio de
![]() engendrado
por las columnas de la matriz
engendrado
por las columnas de la matriz ![]() , está, pues, bien definida y es una biyección
del conjunto cuociente
, está, pues, bien definida y es una biyección
del conjunto cuociente
![]() sobre
sobre
![]() .
Mediante
dicha biyección convenimos en identificar los dos últimos conjuntos y escribimos simplemente:
.
Mediante
dicha biyección convenimos en identificar los dos últimos conjuntos y escribimos simplemente:
Si
![]() y
y
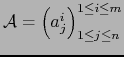 , consideramos
el índice superior
, consideramos
el índice superior ![]() como el ``primero'' de los índices
como el ``primero'' de los índices ![]() y arreglamos los elementos
y arreglamos los elementos
![]() lexicográficamente. Vale decir identificamos la matriz
lexicográficamente. Vale decir identificamos la matriz ![]() con el
elemento
con el
elemento
![]() de
de
![]() .
Escribiremos:
.
Escribiremos:
Demostración
Sea
![]() . Ya que
. Ya que ![]() considerado como matriz de tipo
considerado como matriz de tipo
![]() es de rango
es de rango ![]() , por la ``consecuencia'' del teorema 1.4.19,
, por la ``consecuencia'' del teorema 1.4.19, ![]() posee un menor de orden
posee un menor de orden ![]() distinto de cero, o sea
distinto de cero, o sea
![]() tal que
tal que
![]() y el menor
y el menor
![]() de
de ![]() es distinto de cero.
es distinto de cero.
![]() designamos
por
designamos
por
![]() el correspondiente menor de la matriz
el correspondiente menor de la matriz ![]() . La función
. La función
![]() es
continua, pues, es una función polinomial en los elementos
es
continua, pues, es una función polinomial en los elementos ![]() de la matriz
de la matriz ![]() . Luego
existe una vecindad
. Luego
existe una vecindad ![]() del punto
del punto ![]() en
en
![]() tal que
tal que
![]() .
De ahí
.
De ahí
![]() o sea
o sea
![]() es una vecindad del
punto
es una vecindad del
punto ![]() en
en
![]() . Así viene probado que
. Así viene probado que
![]() es una vecindad de cualquiera de sus puntos, o sea, es un conjunto abierto.
es una vecindad de cualquiera de sus puntos, o sea, es un conjunto abierto.
![]()
De aquí en adelante consideraremos
![]() como espacio topológico,
a saber, lo consideraremos como provisto de la topología inducida por la (usual) de
como espacio topológico,
a saber, lo consideraremos como provisto de la topología inducida por la (usual) de
![]() sobre
sobre
![]() tratado como parte de
tratado como parte de
![]() .
.
A su vez, consideraremos
![]() como espacio topológico, a saber,
el espacio cuociente del espacio topológico
como espacio topológico, a saber,
el espacio cuociente del espacio topológico
![]() por la relación de
equivalencia
por la relación de
equivalencia ![]() .
.
Demostración
Si ![]() es una matriz
es una matriz ![]() inversible, la aplicación
inversible, la aplicación
![]() es un homeomorfismo del
es un homeomorfismo del
![]() sobre sí (ver las relaciones (10) de este ejemplo).
Luego si
sobre sí (ver las relaciones (10) de este ejemplo).
Luego si ![]() es un abierto en
es un abierto en
![]() ,
,
![]() es también
un abierto en
es también
un abierto en
![]() . El saturado del conjunto
. El saturado del conjunto ![]() es la reunión de
todos los conjuntos
es la reunión de
todos los conjuntos
![]() cuando
cuando ![]() recorre la colección
de todas las matrices
recorre la colección
de todas las matrices ![]() inversibles. Dicho saturado es, pues, también abierto
en
inversibles. Dicho saturado es, pues, también abierto
en
![]() .
.
![]()
Resultado 3. Sean ![]() un espacio topológico y
un espacio topológico y ![]() una relación de equivalencia abierta
en
una relación de equivalencia abierta
en ![]() . El espacio topológico cuociente
. El espacio topológico cuociente ![]() es un espacio separado si y sólo
si la gráfica
es un espacio separado si y sólo
si la gráfica ![]() de la relación
de la relación ![]() (es decir el conjunto de todos los
pares
(es decir el conjunto de todos los
pares
![]() tales que
tales que ![]() según
según ![]() ) es un conjunto
cerrado es el espacio producto
) es un conjunto
cerrado es el espacio producto ![]() .
.
Demostración
La gráfica ![]() de la relación de equivalencia abierta
de la relación de equivalencia abierta ![]() en
en
![]() es el conjunto:
es el conjunto:
Ahora bien,
![]() es un conjunto abierto en:
es un conjunto abierto en:
Basta,
pues, mostrar que si
![]() es una
sucesión en
es una
sucesión en ![]() que converge en
que converge en
![]() , como
ahora lo suponemos, a un elemento
, como
ahora lo suponemos, a un elemento
![]() , entonces dicho elemento pertenece a
, entonces dicho elemento pertenece a ![]() .
.
Nuestra hipótesis equivale a:
O sea,
para ![]() ,
,
![]() es una matriz inversible
es una matriz inversible ![]() .
.
De las relaciones (10) de este ejemplo, se sigue inmediatamente:
Observación
El espacio topológico
![]() posee una base numerable de abiertos,
o como diremos brevemente, es un ESPACIO DE BASE NUMERABLE.
posee una base numerable de abiertos,
o como diremos brevemente, es un ESPACIO DE BASE NUMERABLE.
En efecto, puesto que
![]() se identifica con un abierto de
se identifica con un abierto de
![]() ,
,
![]() posee una base numerable de abiertos, digamos
posee una base numerable de abiertos, digamos
![]() . Por ser
. Por ser ![]() una relación de equivalencia abierta de
los abiertos de
una relación de equivalencia abierta de
los abiertos de
![]() son abiertas las imágenes de los abiertos
son abiertas las imágenes de los abiertos
![]() . Luego
. Luego
![]() es una base numerable de abiertos en
es una base numerable de abiertos en
![]() .
.
Resultado 4. Un espacio separado ![]() de base numerable es un espacio compacto si y sólo si
toda sucesión en
de base numerable es un espacio compacto si y sólo si
toda sucesión en ![]() posee una subsucesión convergente en
posee una subsucesión convergente en ![]() .
.
Demostración
Sea
![]() es una sucesión arbitraria en
es una sucesión arbitraria en
![]() . Trabajamos con el
producto escalar canónico en
. Trabajamos con el
producto escalar canónico en
![]() :
:
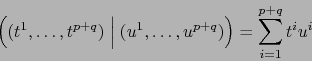
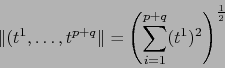
![]() sea
sea
![]() una base
O.N. del subespacio
una base
O.N. del subespacio ![]() de dimensión
de dimensión ![]() de
de
![]() .
.
![]()
![]() es una columna de
es una columna de ![]() números reales. La matriz
números reales. La matriz ![]() de tipo
de tipo
![]() de
columnas
de
columnas
![]() pertenece a
pertenece a
![]() y
y
![]() .
Puesto que
.
Puesto que
![]() , los
elementos de la matriz
, los
elementos de la matriz ![]() tienen valores absolutos menores o iguales a
tienen valores absolutos menores o iguales a ![]() , luego
, luego
![]() es una sucesión acotada en
es una sucesión acotada en
![]() . Por el
teorema de Bolzano-Weierstrass existe una subsucesión
. Por el
teorema de Bolzano-Weierstrass existe una subsucesión
![]() que converge
a un elemento
que converge
a un elemento ![]() de
de
![]() .
.
Construcción de un atlas sobre
![]()
Introducimos, o recordamos, las notaciones siguientes:
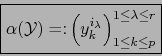
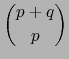 es un recubrimiento de
es un recubrimiento de
![${\cal V}_\alpha = \left\{ {\cal Y} \in {\mbox{\sf H}}_{p,q} \Bigm\vert Y_{[\![ 1,p]\!]}^\alpha \ne 0 \right\}$](img4664.png) y que
la función
y que
la función
![]() tal que
tal que
![]() definimos:
definimos:
Demostración
Toda matriz equivalente a ![]() es de la forma
es de la forma ![]() con
con
![]() ,
inversible. Por la fórmula (18):
,
inversible. Por la fórmula (18):
Observación
Si
![]() , claramente son equivalentes a pares
las afirmaciones:
, claramente son equivalentes a pares
las afirmaciones:
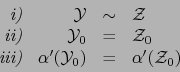
Explícitamente (usando la fórmula (18)).
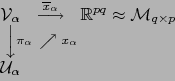
Por la observación después de la proposición 5.4.5, la aplicación ![]() es inyectiva.
es inyectiva.
Sea
![]() la aplicación definida como sigue:
Si
la aplicación definida como sigue:
Si
![]() , sea
, sea
![]() la matriz
la matriz
![]() tal que
tal que
![]() y
y
![]() . Claramente
. Claramente
![]() , vale
, vale
![]() y
y
![]() . Vale, pues:
. Vale, pues:
Demostración
A) Sea ![]() la relación de equivalencia inducida por
la relación de equivalencia inducida por
![]() sobre
sobre
![]() . Ya que
. Ya que
![]() es abierto saturado en
es abierto saturado en
![]() , por el resultado 2,
, por el resultado 2,
![]() puede identificarse como espacio
topológico con el espacio cuociente
puede identificarse como espacio
topológico con el espacio cuociente
![]() y
y ![]() con
la proyección canónica
con
la proyección canónica
![]() .
.
En virtud del resultado 1 quedará probado que ![]() es una aplicación continua, si mostramos
que
es una aplicación continua, si mostramos
que
![]() es continua.
es continua.
Pero por la relación (21) y la aplicación 2) del teorema 1.4.18 vemos que los elementos
de la matriz
![]() , donde
, donde
![]() , son funciones
racionales en los elementos de la matriz
, son funciones
racionales en los elementos de la matriz ![]() , luego la aplicación
, luego la aplicación
![]() es continua y
también
es continua y
también
![]() es continua.
es continua.
B) La relación (22) puede escribirse equivalentemente:
De A) y B) resulta que la aplicación ![]() es un homeomorfismo de
es un homeomorfismo de
![]() sobre
sobre
![]() .
.
![]()
Demostración
Supongamos
![]() y consideremos el cambio de
mapa:
y consideremos el cambio de
mapa:
Conclusión
El atlas
![]() define sobre
define sobre
![]() la estructura de una variedad de clase
la estructura de una variedad de clase ![]() de dimensión pq.
de dimensión pq.
![]() provisto de esta estructura se llama una VARIEDAD GRASSMANIANA.
provisto de esta estructura se llama una VARIEDAD GRASSMANIANA.
Demostración
Manteniendo las notaciones anteriores, designamos por ![]() la proyección canónica
de
la proyección canónica
de
![]() sobre
sobre
![]() . Análogamente a la definición de los
abiertos
. Análogamente a la definición de los
abiertos
![]() de
de
![]() introducimos
introducimos
![]() tal que
tal que
![]() el abierto
el abierto
Sea
![]() tal que
tal que
![]() . Sea
. Sea
![]() . Existe una
única matriz
. Existe una
única matriz
![]() tal que
tal que
![]() y
y
![]() (matriz unidad
(matriz unidad ![]() ). Escribimos explícitamente
). Escribimos explícitamente
![]() con
con
![]() y
y
![]() con
con
![]() . Los vectores columnas
. Los vectores columnas
![]() de la matriz
de la matriz
![]() son:
son:
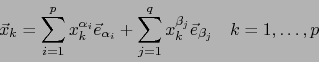
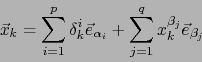
Con esto, hemos probado la afirmación (26).
Sean ![]() y
y ![]() las restricciones de la aplicación
las restricciones de la aplicación
![]() a sendos conjuntos
a sendos conjuntos
![]() y
y
![]() . Sabemos ahora que
. Sabemos ahora que
![]() . Por
simetría
. Por
simetría
![]() . Por el teorema 3.1.10:
. Por el teorema 3.1.10:
De ahí, por el teorema 5.3.6, la restricción a
![]() de la aplicación
de la aplicación
![]() es un isomorfismo
es un isomorfismo ![]() de
de
![]() sobre
sobre
![]() .
.
![]()
Antes de presentar el último ejemplo de esta sección, vamos a exponer un método general para construir variedades diferenciables.
Demostración
Unicidad.
Al suponer que existe una topología deseada sobre ![]() , un subconjunto
, un subconjunto ![]() de
de ![]() será abierto en ella, si y sólo si
será abierto en ella, si y sólo si
![]() es abierto en
es abierto en ![]()
![]() .
Ya que
.
Ya que ![]() es un homeomorfismo de
es un homeomorfismo de ![]() sobre
sobre
![]() , esto ocurre
si y sólo si
, esto ocurre
si y sólo si
![]() es abierto en
es abierto en
![]() , equivalentemente en
, equivalentemente en ![]() . De
ahí la unicidad de dicha topología sobre
. De
ahí la unicidad de dicha topología sobre ![]() .
.
Existencia.
Sea ![]() la colección de todos los subconjuntos
la colección de todos los subconjuntos ![]() de
de ![]() tales que
tales que
![]() es abierto en
es abierto en ![]() .
.
Claramente
![]() y
y ![]() .
.
A. Sea
![]() una familia arbitraria de subconjuntos de
una familia arbitraria de subconjuntos de ![]() , formada por elementos
de
, formada por elementos
de ![]() .
.
![]() tenemos:
tenemos:

B. Sea
![]() una familia finita de subconjuntos de
una familia finita de subconjuntos de ![]() , formada por elementos de
, formada por elementos de ![]() .
.
![]() tenemos:
tenemos:
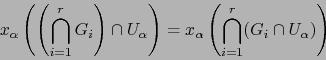
Los resultados A) y B) muestran que la colección ![]() satisface los axiomas
de la colección de abiertos de una topología sobre
satisface los axiomas
de la colección de abiertos de una topología sobre ![]() . De aquí en adelante
consideraremos
. De aquí en adelante
consideraremos ![]() provisto de la topología cuya colección de abiertos es
provisto de la topología cuya colección de abiertos es ![]() .
.
C. Mostremos que
![]() es abierto en
es abierto en ![]() .
Según la definición de la topología sobre
.
Según la definición de la topología sobre ![]() esto significa que
esto significa que
![]() es abierto en
es abierto en ![]() . Se cumple trivialmente si
. Se cumple trivialmente si
![]() ,
mientras que si
,
mientras que si
![]() , esto es precisamente lo que
afirma la hipótesis a) del teorema.
, esto es precisamente lo que
afirma la hipótesis a) del teorema.
D. Probemos que
![]() es una aplicación abierta de
es una aplicación abierta de ![]() sobre
sobre
![]() .
.
Sea ![]() un abierto en
un abierto en ![]() , luego también en
, luego también en ![]() . Por definición de la
topología de
. Por definición de la
topología de ![]() ,
,
![]() :
:
![]() es abierto en
es abierto en
![]() . Al tomar
. Al tomar
![]() vemos que:
vemos que:
E. Queda por probar que ![]() :
: ![]() es una aplicación continua de
es una aplicación continua de
![]() sobre
sobre
![]() .
.
Sea ![]() un abierto en
un abierto en
![]() . Debemos averiguar que
. Debemos averiguar que
![]() es un abierto en
es un abierto en ![]() , es decir, por definición de la topología
de
, es decir, por definición de la topología
de ![]() :
:
Ahora bien por ser ![]() una biyección de
una biyección de
![]() sobre
sobre ![]() , vale:
, vale:
Observación 1
Si
![]() y el recubrimiento
y el recubrimiento
![]() posee un subrecubrimiento
a lo sumo numerable, el espacio topológico
posee un subrecubrimiento
a lo sumo numerable, el espacio topológico ![]() construído por el teorema 5.4.3 es de base
numerable.
construído por el teorema 5.4.3 es de base
numerable.
Demostración
Sin pérdida de generalidad supondremos que el recubrimiento
![]() es a lo sumo
numerable.
es a lo sumo
numerable.
Puesto que
![]() ,
, ![]() es homeomorfo a un abierto
de
es homeomorfo a un abierto
de
![]() ,
, ![]() posee una base numerable de abiertos, digamos
posee una base numerable de abiertos, digamos
![]() . La colección
. La colección
![]() es patentemente una base numerable
de abiertos del espacio
es patentemente una base numerable
de abiertos del espacio ![]() .
. ![]()
Observación 2
Supongamos que el espacio ![]() en el enunciado del teorema 5.4.3 es
en el enunciado del teorema 5.4.3 es
![]() y reforcemos
la condición b) de dicho enunciado subsituyéndola por la siguiente:
y reforcemos
la condición b) de dicho enunciado subsituyéndola por la siguiente:
Si
![]() la aplicación
la aplicación
Entonces ![]() (junto con el atlas admisible
(junto con el atlas admisible
![]() ) es una variedad
) es una variedad
![]() de dimensión
de dimensión ![]() .
.
Nota
En lenguaje informal podemos decir que la topología de una variedad diferenciable
está definida sin ambigüedad por un atlas admisible de ésta.
Mejor dicho: Para construir una variedad diferenciable ![]() podemos construir lo que
resultará ser su atlas admisible por el principio de la pegadura de trozos. La topología de
podemos construir lo que
resultará ser su atlas admisible por el principio de la pegadura de trozos. La topología de ![]() se dará por añadidura.
se dará por añadidura.