




Siguiente: La funcional
Arriba: Diferenciación en espacios afines
Anterior: Diferenciales de funciones reales
Advertencia
Las aplicaciones i) y ii) no hacen de 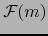 un álgebra y ni siquiera un espacio vectorial sobre
un álgebra y ni siquiera un espacio vectorial sobre 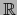 .
.
Se ve, por ejemplo, inmediatamente, que la única función
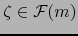 la cual actúa como cero en la adición, es decir, cumple
la cual actúa como cero en la adición, es decir, cumple
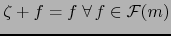 es la función
es la función
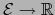 de valor
de valor 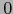 en
en  .
.
Si
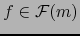 tiene
dominio
tiene
dominio 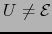 , el dominio de
, el dominio de
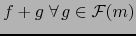 es un subconjunto de
es un subconjunto de 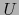 , luego no existe
, luego no existe
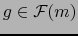 tal que
tal que 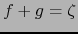 .
.
Se puede también notar que si 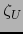 es la función en
es la función en
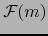 de dominio
de dominio 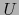 y de valor cero en él, se tiene para nuestra
y de valor cero en él, se tiene para nuestra 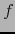 :
: 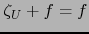 sin que sea
sin que sea
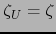 .
.
Demostración
La afirmación a) se sigue del teorema 4.3.2.
La afirmación b) la daremos aquí por conocida. Las simples demostraciones, si éste no las tiene presentes, las dejamos al lector.
La afirmación c) sigue de los incisos a) y b) del teorema 4.3.5.
La afirmación d) sigue del inciso c) del mismo teorema 4.3.5. 





Siguiente: La funcional
Arriba: Diferenciación en espacios afines
Anterior: Diferenciales de funciones reales
Guillermo M. Luna
2009-06-14
 una aplicación
una aplicación
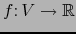 , donde
, donde 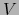 es
una vecindad abierta de m en
es
una vecindad abierta de m en  que depende de la función
que depende de la función 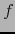 .
Designaremos por
.
Designaremos por 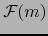 el conjunto de todas las funciones locales en el punto
el conjunto de todas las funciones locales en el punto  .
.
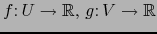 funciones locales en m y sean
funciones locales en m y sean
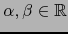 .
.
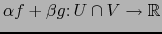 por
por
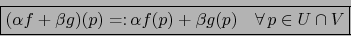
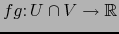 por:
por:
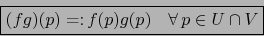
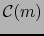 el subconjunto de
el subconjunto de 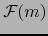 constituido por las funciones locales en
constituido por las funciones locales en  continuas en el punto
continuas en el punto  .
.
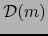 el subconjunto de
el subconjunto de 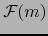 constituido por las funciones locales en
constituido por las funciones locales en  diferenciables en el punto
diferenciables en el punto  .
.