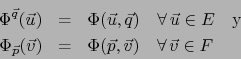Siguiente: Una lista de resultados
Arriba: Más sobre diferenciales
Anterior: Productos de espacios afines
Sean
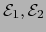 espacios afines normados y
espacios afines normados y
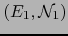 ,
,
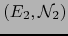 sus respectivos espacios vectoriales asociados de
sendas normas
sus respectivos espacios vectoriales asociados de
sendas normas
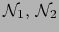 . Sea
. Sea  la norma inducida sobre el espacio vectorial producto
la norma inducida sobre el espacio vectorial producto
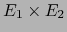 .
Sean
.
Sean
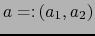 un punto de
un punto de
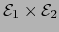 y
y 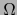 una vecindad abierta de
una vecindad abierta de 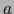 en
en
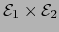 .
.
Puesto que
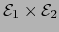 es el producto topológico de los espacios
es el producto topológico de los espacios  ,
,  , existen vecindades
abiertas
, existen vecindades
abiertas 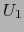 de
de 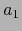 en
en  y
y 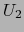 de
de 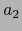 en
en  tales que
tales que
 .
.
Consideramos una aplicación
 donde
donde 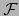 es un espacio afín normado, de espacio vectorial asociado
es un espacio afín normado, de espacio vectorial asociado  .
.
Definimos las APLICACIONES PARCIALES
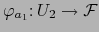 y
y
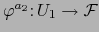 por las fórmulas:
por las fórmulas:
Si la aplicación 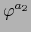 es diferenciable en el punto
es diferenciable en el punto 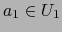 ponemos:
ponemos:
Si la aplicación  es diferenciable en el punto
es diferenciable en el punto 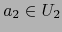 ponemos:
ponemos:
Las aplicaciones lineales continuas
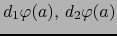 , si existen, se llaman las DIFERENCIALES PARCIALES DE LA APLICACIÓN EN EL PUNTO .
, si existen, se llaman las DIFERENCIALES PARCIALES DE LA APLICACIÓN EN EL PUNTO .
Demostración
Sean
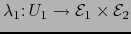 y
y
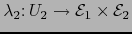 las aplicaciones:
las aplicaciones:
Se verifica:
Sean
 y
y
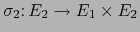 las aplicaciones lineales:
las aplicaciones lineales:
Si
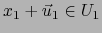 tenemos
tenemos
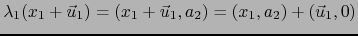 o sea,
o sea,
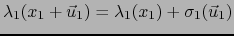 .
Asimismo, si
.
Asimismo, si
 , entonces
, entonces
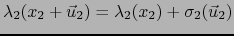 .
.
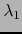 es, pues, restricción a
es, pues, restricción a 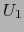 de una aplicación afín de parte lineal
de una aplicación afín de parte lineal  y
y
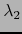 es restricción a
es restricción a 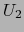 de una aplicación afín de parte lineal
de una aplicación afín de parte lineal  .
.
Puesto que:
las aplicaciones lineales  ,
,  son continuas.
son continuas.
Del teorema 4.3.4 se sigue ahora que 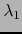 es diferenciable en
es diferenciable en 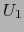 y
y 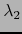 en
en 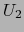 siendo:
siendo:
Se sigue de (6) y (7) y de la regla de la cadena (teorema 4.4.4) que 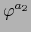 es diferenciable
en
es diferenciable
en 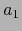 , o sea, existe
, o sea, existe
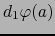 y
y  es diferenciable en
es diferenciable en 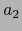 o sea existe
o sea existe
 , siendo por cierto:
, siendo por cierto:
De ahí :
Finalmente, sumando las dos últimas relaciones:

Advertencia
El recíproco de la última proposición es falso:
la existencia de las dos diferenciales parciales
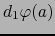 ,
,
 no implica
la diferenciabilidad de la aplicación
no implica
la diferenciabilidad de la aplicación  en a.
en a.
Para 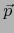 y
y 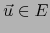 y para
y para
 escribamos:
escribamos:
 |
(8) |
La aplicación
 es una aplicación lineal continua de
es una aplicación lineal continua de 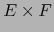 en
en 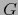 .
También, por la ``generalización'' del teorema 4.2.5,(enunciado después del teorema 4.2.6) existe
.
También, por la ``generalización'' del teorema 4.2.5,(enunciado después del teorema 4.2.6) existe  tal que
tal que
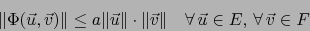 |
(9) |
De (9) se sigue a fortiori:
de donde:
Dado esto por sentado, la fórmula (8) prueba el teorema.

Nota
Con las notaciones antes del teorema 4.4.8, tenemos:
La aplicación
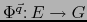 es lineal continua. Luego, por el corolario del teorema 4.3.4:
es lineal continua. Luego, por el corolario del teorema 4.3.4:
Asimismo:
La fórmula en el teorema 4.4.9 es, pues, un caso particular de aquélla en el teorema 4.4.8. Pero no pudimos aplicar
el teorema 4.4.8 sin saber de antemano que 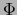 es diferenciable en el punto
es diferenciable en el punto
 .
.





Siguiente: Una lista de resultados
Arriba: Más sobre diferenciales
Anterior: Productos de espacios afines
Guillermo M. Luna
2009-06-14
![]() espacios afines normados y
espacios afines normados y
![]() ,
,
![]() sus respectivos espacios vectoriales asociados de
sendas normas
sus respectivos espacios vectoriales asociados de
sendas normas
![]() . Sea
. Sea ![]() la norma inducida sobre el espacio vectorial producto
la norma inducida sobre el espacio vectorial producto
![]() .
Sean
.
Sean
![]() un punto de
un punto de
![]() y
y ![]() una vecindad abierta de
una vecindad abierta de ![]() en
en
![]() .
.
![]() es el producto topológico de los espacios
es el producto topológico de los espacios ![]() ,
, ![]() , existen vecindades
abiertas
, existen vecindades
abiertas ![]() de
de ![]() en
en ![]() y
y ![]() de
de ![]() en
en ![]() tales que
tales que
![]() .
.
![]() donde
donde ![]() es un espacio afín normado, de espacio vectorial asociado
es un espacio afín normado, de espacio vectorial asociado ![]() .
.
![]() y
y
![]() por las fórmulas:
por las fórmulas:
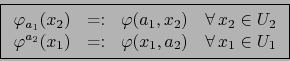
![]() y
y
![]() las aplicaciones:
las aplicaciones:
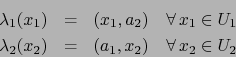
![]() es, pues, restricción a
es, pues, restricción a ![]() de una aplicación afín de parte lineal
de una aplicación afín de parte lineal ![]() y
y
![]() es restricción a
es restricción a ![]() de una aplicación afín de parte lineal
de una aplicación afín de parte lineal ![]() .
.
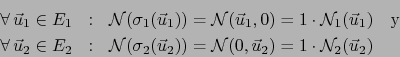
![]() es diferenciable en
es diferenciable en ![]() y
y ![]() en
en ![]() siendo:
siendo:
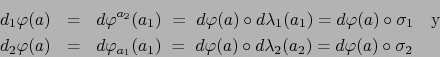
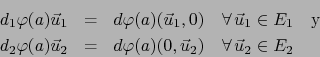
![]() ,
,
![]() no implica
la diferenciabilidad de la aplicación
no implica
la diferenciabilidad de la aplicación ![]() en a.
en a.