




Siguiente: Mapas y atlas admisibles.
Arriba: Cálculo en variedades diferenciales
Anterior: Isomorfismos
A partir de este capítulo haremos un uso (moderado) de
topología general. Emplearemos la siguiente:
Terminología (N. Bourbaki)
- Un espacio topológico
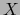 se dice ESPACIO SEPARADO si
satisface el siguiente AXIOMA DE HAUSDORFF o un axioma equivalente:
se dice ESPACIO SEPARADO si
satisface el siguiente AXIOMA DE HAUSDORFF o un axioma equivalente:
Dos puntos distintos arbitrarios de 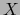 poseen sendas vecindades ajenas.
poseen sendas vecindades ajenas.
- Un espacio topológico
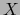 se dice ESPACIO COMPACTO si:
se dice ESPACIO COMPACTO si:
- es separado,
- satisface el siguiente AXIOMA DE BOREL-LEBESGUE o un axioma
equivalente.
Todo recubrimiento abierto de 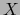 contiene un subrecubrimiento
finito de
contiene un subrecubrimiento
finito de 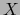
- Un espacio topológico
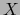 se dice ESPACIO LOCALMENTE COMPACTO si
se dice ESPACIO LOCALMENTE COMPACTO si
- es separado, y
- todo punto de
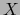 posee una vecindad compacta.
posee una vecindad compacta.
La mayoría de los autores anglosajones omiten la exigencia de separación
en las definiciones b) y c). Esta omisión es inconveniente especialmente en
el caso de la definición c), pues, un espacio que ellos llaman ``localmente
compacto '', si no es separado, no tiene prácticamente ningunas propiedades
interesantes. Esto obliga a los mencionados autores a hablar constantemente de
espacios localmente compactos ``de Hausdorff'', es decir, separados. Tal costumbre
es algo molesta y poco estética. Una crítica semejante aunque en grado
menor, vale para la definición b) con omisión de la condición de
separación.
Un espacio no necesariamente separado, que satisface el axioma de Borel-Lebesgue,
se llama según Bourbaki, un ESPACIO CASI COMPACTO.
Subsections





Siguiente: Mapas y atlas admisibles.
Arriba: Cálculo en variedades diferenciales
Anterior: Isomorfismos
Guillermo M. Luna
2009-06-14
poseen sendas vecindades ajenas.
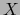 posee una vecindad compacta.
posee una vecindad compacta.
poseen sendas vecindades ajenas.