


Next: About this document Up: Autómatas Celulares Lineales Reversibles Previous:
Referencias
- Vecindad de von Neumann.
- Vecindad de Moore.
- ACL donde cada célula tiene un vecino a cada
lado (r=1), el tamaño total de la vecindad es 2r+1=3.
- Cadena de células dispuesta en forma de
anillo.
- Forma en que evoluciona la i- ésima
célula en un ACL(k,1).
- Forma en que evoluciona la i- ésima
célula en un ACL(k,h), h= 0.5.
- ACL's Clase 1.
- ACL's Clase 2.
- ACL's Clase 3.
- ACL's Clase 4.
- Ordenación de una secuancia aleatoria de
0's y 1's con un ACL(3,1) regla QD3QD3Q03.
- Ordenación `` paralela'' de
secuancias aleatorias de 0's y 1's con un ACL.
- Diagrama de de Bruijn de un ACL(2,1) regla
90.
- Diagrama de de Bruijn renombrado de un
ACL(2,1) regla 90.
- Diagrama de de Bruijn de un ACL(4,h) regla
0F08725C.
- Diagrama de de Bruijn de un ACL(2,1) regla
22.
- Diagrama de Subconjuntos de un ACL(2,1)
regla 22.
- Diagrama de Parejas de un ACL(2,1) regla 22.
- Evolución de una configuracón de 2
células de un ACL(4,h) regla EC78946E.
- Evolución de una configuracón de 3
células de un ACL(4,h) regla EC78946E.
- Evolución de una configuracón de 4
células de un ACL(4,h) regla EC78946E.
- Evolución de un ACL(4,h) regla EC78946E,
donde cadenas de dos o más
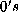 son parte del Jardín
del Edén de tal ACL.
son parte del Jardín
del Edén de tal ACL.
- Diferentes tipos de mapeo de una función.
- La regla de evolución de un ACLR define un
automorfismo.
- Configuraciones de tamaño 2 que evolucionan
en 0.
- Configuraciones de tamaño 3 que evolucionan
en 02.
- Conjunto de ancestros de las configuraciones
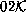 .
.
- Elementos del conjunto
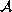 de cadenas que evolucionan en 02 que forman los ancestros de
la configuración 02102.
de cadenas que evolucionan en 02 que forman los ancestros de
la configuración 02102.
- Regla de evolución 0067A26CIJOOI de un
ACLR(5,h), y las extensiones derechas compatibles con 0 que evolucionan en 3
y 4.
- Extensiones derechas compatibles con 0
que evolucionan en 34 y 40.
- Extensiones derechas compatibles con 0
que evolucionan en 342.
- Extensiones izquierdas compatibles con 0
que evolucionan en 3 y 4.
- Extensiones izquierdas compatibles con 0
que evolucionan en 23 y 14.
- Ancestros de la cadena 231.
- Ancestros de la cadena 130.
- Ejemplos de ACLR y sus valores de LMR.
- Ejemplos de ACLR con valores de LMR
no primos.
- ACL no reversible (5,h) con cadenas cuyas
valores de
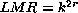 .
.
- Ancestros de la cadena formada alternando
los estados 0,2.
- Ancestros de la cadena formada alternando
los estados 1,4.
- ACLR(5,h) donde el valor de M siempre
es igual a 1.
- ACL(5,h) no reversibles y parte de sus
diagramas de de Bruijn asociados.
- ACLR(5,h) regla 0067A26CIJOOI y la ruta 332
en su diagrama de de Bruijn.
- ACLR(2,1) regla 85 y su diagrama de parejas
asociado.
- ACLR(3,h) regla 8229 y su diagrama de
parejas asociado.
- ACL(2,1) regla 231 y su diagrama de
subconjuntos.
- ACLR(5,h) regla 00077HIGLBDOO y su diagrama
de subconjuntos.
- ACLR(5,h) regla 000667CCIJOOI y su diagrama
de subconjuntos.
- ACLR(5,h) reflexión de la regla
000667CCIJOOI y su diagrama de subconjuntos.
- ACL(5,h) regla 4ODIJLCH16700 donde existen
ciclos en el diagrama de subconjuntos y en el de parejas.
- ACL(2,1) regla 253 en donde la cadena de
estados 00 pertenece al Jardín del Edén.
- ACL(4,h) regla 4EB11BE4 el cual tiene un
mapeo global sobreyectivo pero no reversible.
- ACLR(4,h) regla 05AF05AF.
- ACLR(2,1) regla 51.
- ACLR(5,h) regla 3CDK0KL56O7IH.
- ACLR(2,1) regla 240.
- Utilizando el método de Fredkin en la
evolución de una configuración aleatoria en un ACLR(2,1) regla 240.
- Regla 240 de un ACLR(2,1) y su regla
inversa obtenida por el método de Fredkin.
- Usando el método de Fredkin con suma y
resta módulo 3.
- Evolución del ACLR(3,h) regla 10179 y de
su regla inversa 11355.
- ACL(3,h) regla 6007.
- ACL(3,h) regla 14007.
- ACL(3,h) regla 2119.
- Ancestro único de la cadena 01 que
puede representarse con la misma longitud.
- Verificación de que cada cadena tenga un
único elemento en común en el pasado para cadenas de longitud 2, 3 y 4.
- ACLR(4,h) regla FF5500AA.
- Cluster mínimo del ACLR(4,h) regla
FF5500AA.
- Cluster mínimo de varios ACLR(4,h).
- ACL(4,h) con múltiples ancestros para una
cadena de 1's.
- ACL(2,1) con múltiples ancestros para una
cadena de 0's.
- Matriz de conectividad del estado 0
del ACLR(3,h) regla 715 y como se manifiesta los índices de Welch en ésta.
- Diagramas de subconjuntos y valores de L,
M y R para la matriz de conectividad del estado 0 del ACLR(3,h) regla
715.
- Diagramas de subconjuntos (regla original
y reflejada) del ACLR(3,h) regla 715.
- Indices de Welch para la cadena 01
del ACLR(3,h) regla 9711.
- Diferentes formas de matrices de
conectividad para ACLR, con un solo 1 en la diagonal principal y valores de
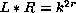 induciendo que M=1.
induciendo que M=1.
- Matrices de conectividad para ACL no
reversibles.
- Matriz de rutas del estado 0 en un
ACL(4,h) donde se observan múltiples ancestros.
- Matriz de rutas del estado 0 y 1
en un ACL(4,h) donde se observan múltiples ancestros.
- Crecimiento del número de matrices de
conectividad a revisar para cadenas de longitud 1 en adelante para un ACL(4,h).
- Flujo del proceso para obtener ACLR(k,r).
- ACLR(4,h) con L=1 y R=4.
- ACLR(4,h) con L=2 y R=2.
- ACLR(5,h) con L=1 y R=5.
- ACLR(5,h) con L=1 y R=5.
- ACLR(6,h) con L=1 y R=6.
- ACLR(6,h) con L=1 y R=6.
- ACLR(6,h) con L=1 y R=6.
- ACLR(6,h) con L=2 y R=3.
- ACLR(6,h) con L=2 y R=3.
- ACLR(6,h) con L=2 y R=3.
Seck Tuoh Mora Juan Carlos
E-mail:seck@delta.cs.cinvestav.mx
![]()