CINVESTAV-I.P.N.
Resumen
El tránsito de automóviles en ciudades y carreteras es un problema que cada
día tiene mayor importancia y requiere de estudios profundos que puedan
ser puestos dentro del contexto de sistemas complejos. Para el análisis del
flujo de tránsito de autos, se han creado diversos modelos basados en
teorías relacionadas con matemáticas y física (Car-Following,
Autómatas Celulares, Dinámica de Fluidos, Teoría de Colas, Teoría
Cinética de Gases). Estos modelos han sido simulados en computadora para
poder predecir comportamientos bajo diferentes escenarios. En la actualidad las
simulaciones se realizan tomando como dichos escenarios diversas ciudades del
mundo.
El objetivo de esta tesis es presentar un análisis del
problema del flujo de tránsito de autos utilizando herramientas de
teoría de gráficas en autómatas celulares. Las herramientas de
teoría de gráficas utilizadas en esta tesis son los diagramas de Bruijn,
de subconjuntos y de ciclos. Para incorporar dichas herramientas al análisis
se estableció como punto de partida la regla de AC(2,1) 184 por ser el modelo
que simula flujo de tránsito de autos con la dinámica más sencilla.
Posteriormente, se tomó como base el modelo creado por Kai Nagel, el cual es
representado por un autómata celular que reproduce el flujo de tránsito de
autos en una dimensión y en una dirección. Se propone un método para
poder utilizar los diagramas de Bruijn, de subconjuntos y de ciclos debido a
que el modelo original de Nagel no permite de manera directa la utilización
de dichos diagramas. El método consiste en la indentificación de reglas o
autómatas celulares basados en la notación de Wolfram. Estas reglas deben
tener un comportamiento equivalente al modelo de Nagel. La primer regla que se
presenta es la 43, la cual es representada por un autómata celular de orden
(2,1). Se encontró que esta regla no incluye todas las configuraciones de
autos que se pueden presentar en la carretera en el caso de que la velocidad
máxima que pueden alcanzar éstos sea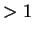 
. Posteriormente, se presenta una
regla representada por un autómata celular de orden (4,2), la cual sí
incluye todas las configuraciones posibles cuando el modelo contempla dos
velocidades. A este autómata celular se le denominó LCATRAFFICFLOWVMAX2.
LCATRAFFICFLOWVMAX2 tiene un comportamiento equivalente al modelo de
Nagel cuando la velocidad máxima que pueden alcanzar los autos es igual a 2,
con la diferencia que nuestro modelo es completamente determinístico. La
ventaja que tiene LCATRAFFICFLOWVMAX2 es que se puede predecir o analizar su
comportamiento aún antes de llevar a cabo una simulación en computadora.
Esto es posible utilizando las herramientas de teoría de gráficas antes
citadas.
El utilizar herramientas gráficas nos permite realizar
un estudio
amplio de LCATRAFFICFLOWVMAX2 de manera confiable y funcional sin tener por
necesidad que contar con un gran equipo de potentes computadoras para llevar a
cabo simulaciones.
De tal forma, en este documento se describen
algunos modelos y se explican los conceptos básicos de la teoría de
flujo de tránsito de autos. También se hace una descripción general de
los conceptos referentes a la teoría de autómata celular. Se presenta el
estudio realizado de las reglas de AC(2,1) 184, 43, y de la regla de AC(4,2)
LCATRAFFICFLOWVMAX2. Por último, se muestra un programa realizado en el
manejador de base de datos PROGRESS que ilustra el comportamiento de nuestro
modelo LCATRAFFICFLOWVMAX2.